The Concept of Interval in Music
The concept of 'interval' is easily understood when thought of in terms of time or space. It is a gap in time or space between two things, such as the short break between the acts of a play or long film, or the distance of, say, 10 feet between two posts.
But in music, the concept is a little deeper: to say it is the difference in pitch between two notes or tones is correct, but is not as easy to calculate as is a number of seconds or feet.
The reason for this is the nature of what we are considering: sound. This phenomenon is caused by vibrating air particles. The source of any sound must mechanically vibrate in order to move the air that is physically in contact with it. The closely packed air molecules will compress and expand (air being an elastic medium) in accordance with the vibrating frequency of the object. Then, much like a 'slinky' spring, the compression/decompression wave fronts will travel forth with the velocity of sound (332 m/s at 0°C) until they reach, say, an eardrum. Here, they will set the eardrum in motion at exactly the same frequency of the source, and the listener hears a sound. The higher the vibrational frequency, the higher the pitch. So the interval between two notes, one 'higher' and one 'lower' is a measure of the difference between two frequencies. But, as we shall see, it is not calculated as the higher minus the lower, as could be done with the temporal and spatial examples. Here we are dealing with a non-linear phenomenon!
If our ears were exposed to a pure, single-note sound, and we were to measure the air pressure on our eardrum as a function of time, we would obtain the graph of a sine wave. Maximum pressure events would occur at regular intervals and with a unique frequency (f1), and our brain's auditory cortex would perceive a certain sound. Now if a second sound (with frequency f2) were generated by another sound source, having exactly twice the frequency of the first, then the frequency of high pressure events on the eardrum would also exactly double. Because of the extremely simple relationship between the two frequencies (f2 = 2 x f1), the resulting mode of vibration of the eardrum would still be relatively simple, and the two sounds would be perceived as blending very smoothly. However, if f2 were made to be less than twice the frequency of f1, the degree of disturbance with the first sound wave would increase. We thus consider f2 = 2 x f1 the most 'consonant' frequency to f1.
We may also check with mathematical methods that f2 does in fact produce the least disturbance of f1. If we represent both waves as graphs denoting air pressure against time, we obtain two sine waves, one having half the wavelength of the other. If we now add them together (which is the equivalent of superimposing the actual sounds) by simply adding the individual values of pressure at equal points in time, we obtain the graphical representation of the resultant sound. (By the way, in acoustics this is called Fourier analysis). It is immediately evident how adding a sine wave with twice the frequency (and hence half the wavelength) yields the simplest result, compared with adopting any other f2. See Figure 1. Conveniently, all the points of neutral air pressure of f1 (T2, T4, etc.) always coincide exactly with points of neutral air pressure of f2.
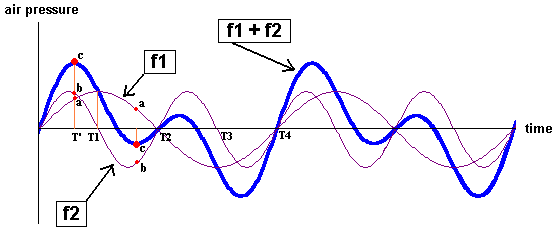Figure 1
It was, in fact, Pythagoras (530 BC) who not only noted the relative consonance of certain pairs of notes (by hearing the beating of anvils with hammers of different weights), but also proceeded to discover that the more consonant pairs of notes are related by simple mathematical relationships: x 2, x 3/2, x 4/3, x 5/4 etc.. We are now ready to investigate the non-linearity of sound behaviour. Consider a note, say the central A on a piano. This is conventionally tuned to 440 cycles per second (or Hz). Our first most consonant note above it must therefore have a frequency of 880 Hz. If we were to add the third most consonant note, we would have to find the note that, in its turn, least disturbed not only 440 Hz, but also 880 Hz. This must be 2 x 880 = 1760 Hz. The scale that emerges is an interesting one. As we move from one consonant note to the next, the frequencies rise exponentially! See Figure 2.
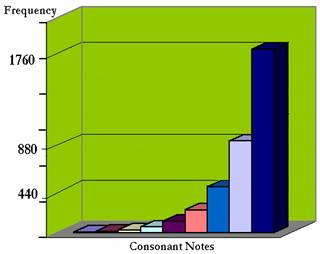
Figure 2
This makes sense, as a linear scale would imply that we could reduce frequency to zero, and this would be impossible: no frequency can be found for which another, slightly lower one cannot be supplied! This is because we are measuring an event that takes place within a fixed time frame, i.e. the second. If I am given one second to do something, there is theoretically no limit to how little (or how much) I can achieve in that second. (Mathematically speaking, the only limit is infinity).
The name 'octave' is given to this primordial sound interval between any two notes having frequencies related by the x 2 function. Through the course of the history of Western music, this octave was divided into 12 parts, and, following the adoption of Equal Temperament (a mathematical method of tuning which enabled Bach to compose his renowned Well Tempered Clavier), these parts were made 'equal'. Prior to this, the octave was NOT divided equally, in an attempt to respect the rules of mathematical consonance.
Before the advent of Equal Temperament, a starting note was chosen. Then the octave was derived. Next, the note corresponding to the 3/2 the frequency of the starting note (the 'so called 'fifth') was derived. Next, the fifth was taken as a new starting note and the fifth above it was derived. This in turn was taken as a new starting point, and so forth, until a collection of differing notes was generated. By the time the twelfth note was generated, something resembling a note 7 octaves above the original note was reached. But mathematics is never that elementary! The two frequencies, regrettably, did not match. In fact, however long we multiply a frequency by 3/2, we will never have the satisfaction of seeing it coincide with the frequency of an octave. The two equations live separate lives, their paths never again to cross after their common origin.
Many methods and approaches have been adopted to overcome this obstacle, but the most sensible to date was that of making every one of the twelve notes within the octave have an equal relationship to its neighbour. Just as any note's frequency can be multiplied by 2 to get the octave above, or divided by 2 to get the octave below, any of the twelve frequencies (notes) within the octave can be multiplied by N (a certain number) to get the frequency (note) immediately above it, or divided by N to get the frequency (note) immediately below it.
This magic number N is the twelfth root of 2 ( = 1.0594630944....). This is not hard to see.
Suppose we start with an initial note having frequency f1. The note above it will have frequency N x f1. The next note will have frequency N x (N x f1), and so forth. But we know that the twelth frequency must equal the octave, or 2f. So we can say that:
2 x f = (N x N x N x N x N x N x N x N x N x N x N x N) x f
12
= N x f
which means:
12
2 = N i.e. N = the twelfth root of 2 (or that number which multiplied by itself 12 times gives 2) !!
In this way we have defined the 'perfect' chromatic scale, or a collection of 12 notes all symmetrically positioned within the octave. It is now possible for us to consider the interval between any pair of adjacent frequencies (notes) and obtain the same ratio.
More interestingly, we may consider a fixed interval between any NON-adjacent pair of frequencies (notes) and again we will obtain the same ratio, irrespective of what note is chosen as the bottom note.
A chord is made up of 3 or more notes sounded together. The intervals which exist between its component notes constitute its very nature or 'character'. In music that modulates to different keys, a particular chord type must preserve its inner intervallic relationships, whatever the base note happens to be. For this reason, this new, correct definition of the chromatic interval was a major breakthrough for the evolution of modern, western music.
References:
1. Harmony Theory and Just Intonation: http://users.rcn.com/dante.interport//hartheory1.html
2. Just vs. Equal Temperament: http://www.phy.mtu.edu/~suits/scales.html
3. Fourier Synthesis: http://www.nst.ing.tu-bs.de/schaukasten/fourier/en_idx.html
4. A Review of Logarithms: http://www.sosmath.com/algebra/logs/log1/log1.html
5. The Physiology of Hearing: http://www.anu.edu.au/ITA/ACAT/drw/PPofM/hearing/hearing1.html
The Elements of Harmony | Baroque Harmony | 4-Part Jazz Harmony | Harmonic Sequences Archive | Percussion | Pythagoras | 4-Part Score Editor | Discussion Forum